Ensamblaje y Solución (Algoritmo Unificado) 🧩

Tabla de contenido

Metodo de la rigidez - Este artículo es parte de una serie.

Parte 1: Fundamentos Teóricos: El Sistema Central 🏛️

Parte 2: Este artículo

Parte 3: Post-Procesamiento y Resultados 📊

II. Ensamblaje y Solución (Algoritmo Unificado) 🧩
#

Una vez que tenemos la Matriz de Rigidez Global del Elemento ($\mathbf{K}_{\text{global}}$) para cada componente de la estructura (como la barra axial $4 \times 4$ vista en la Sección I), el siguiente paso es combinarlas para formar la matriz del sistema completo ($\mathbf{K}$) y luego resolverlo.

1. Ensamblaje de la Matriz Global ($\mathbf{K}$) por Superposición Directa
#

El corazón del Método de la Rigidez reside en el proceso de ensamblaje. Este método se basa en los principios de equilibrio nodal y compatibilidad de desplazamientos.

Principio: La Matriz de Rigidez Global $\mathbf{K}$ del sistema completo se obtiene sumando las contribuciones de rigidez de cada matriz $\mathbf{K}_{\text{global}}$ individual en las posiciones correctas, según cómo los elementos se conectan en los nudos.
Grados de Libertad Globales (GDL): Antes de ensamblar, debemos numerar todos los posibles movimientos (desplazamientos $u_x, u_y$ y rotaciones $\theta_z$ si aplica) en cada nudo de la estructura. Este conjunto forma los GDL globales del sistema. Si hay $N_{nudos}$ y cada nudo tiene $g$ GDL (e.g., $g=2$ para armaduras 2D), la matriz $\mathbf{K}$ tendrá dimensiones $(N_{nudos} \times g) \times (N_{nudos} \times g)$. Por ejemplo, la estructura siguiente tiene 3 elementos y 3 nudos. Cada nudo tiene 2 GDL (Movimiento $u_x, u_y$), por lo que, la matriz $\mathbf{K}$ tendrá dimensiones $(3 \times 2) \times (3 \times 2) = (6 \times 6)$.

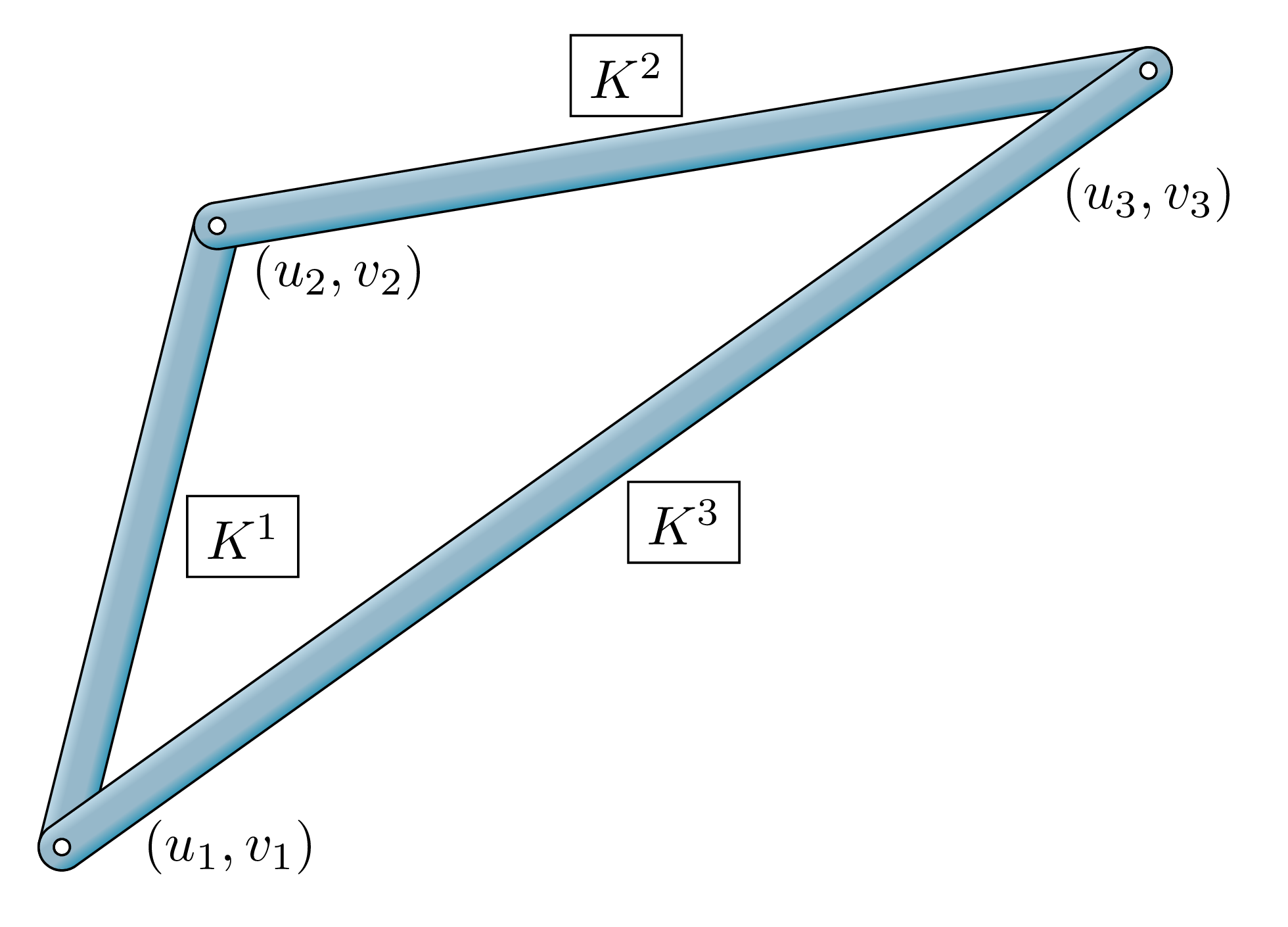
Mapeo y Suma (Superposición):
1. Inicializar $\mathbf{K}$: Crear una matriz global $\mathbf{K}$ llena de ceros, con tamaño igual al número total de GDL globales.
2. Iterar por Elementos: Para cada elemento de la estructura:
  - Calcular su $\mathbf{K}_{\text{global}}$ ($4 \times 4$ para barra axial 2D).
  - Identificar los índices de GDL globales asociados a los nudos de ese elemento. Por ejemplo, si una barra conecta el Nudo 1 (GDL globales 1, 2) y el Nudo 2 (GDL globales 3, 4).
  - Sumar: Añadir cada término $(i, j)$ de la $\mathbf{K}_{\text{global}}$ del elemento al término correspondiente $(I, J)$ de la matriz $\mathbf{K}$ global, donde $I$ y $J$ son los índices globales mapeados desde los índices locales $i$ y $j$.
Ejemplo Conceptual: El proceso se puede desarrollar de la siguiente manera para la figura mostrada más arriba:
1. Inicializar $\mathbf{K}$: $$ \mathbf{K} = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_2\;\; & v_2\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_2} \\ F_{v_2} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} K_{11} & K_{12} & K_{13} & K_{14} & K_{15} & K_{16}\\ K_{21} & K_{22} & K_{23} & K_{24} & K_{25} & K_{26}\\ K_{31} & K_{32} & K_{33} & K_{34} & K_{35} & K_{36}\\ K_{41} & K_{42} & K_{43} & K_{44} & K_{45} & K_{46}\\ K_{51} & K_{52} & K_{53} & K_{54} & K_{55} & K_{56}\\ K_{61} & K_{62} & K_{63} & K_{64} & K_{65} & K_{66} \end{pmatrix} % \end{array} = \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}$$
2.1. Iterar por Elementos (K 1):
$$\mathbf{K^1} = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_2\;\; & v_2\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_2} \\ F_{v_2} \end{matrix} & \begin{pmatrix} K_{11}^1 & K_{12}^1 & K_{13}^1 & K_{14}^1\\ K_{21}^1 & K_{22}^1 & K_{23}^1 & K_{24}^1\\ K_{31}^1 & K_{32}^1 & K_{33}^1 & K_{34}^1\\ K_{41}^1 & K_{42}^1 & K_{43}^1 & K_{44}^1\\ \end{pmatrix} % \end{array} \implies$$$$ \mathbf{K}^1_G = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_2\;\; & v_2\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_2} \\ F_{v_2} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} K_{11}^1 & K_{12}^1 & K_{13}^1 & K_{14}^1 & 0 & 0\\ K_{21}^1 & K_{22}^1 & K_{23}^1 & K_{24}^1 & 0 & 0\\ K_{31}^1 & K_{32}^1 & K_{33}^1 & K_{34}^1 & 0 & 0\\ K_{41}^1 & K_{42}^1 & K_{43}^1 & K_{44}^1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix} % \end{array}$$
Se le suma $\mathbf{K}^1_G$ a la matriz $\mathbf{K}$

2.2. Iterar por Elementos (K 2):
$$\mathbf{K^2} = \begin{array}{cc}% & \begin{matrix} u_2\;\; & v_2\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_2} \\ F_{v_2} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} K_{11}^2 & K_{12}^2 & K_{13}^2 & K_{14}^2\\ K_{21}^2 & K_{22}^2 & K_{23}^2 & K_{24}^2\\ K_{31}^2 & K_{32}^2 & K_{33}^2 & K_{34}^2\\ K_{41}^2 & K_{42}^2 & K_{43}^2 & K_{44}^2\\ \end{pmatrix} % \end{array} \implies$$$$ \mathbf{K}^2_G = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_2\;\; & v_2\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_2} \\ F_{v_2} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 &K_{11}^2 & K_{12}^2 & K_{13}^2 & K_{14}^2 \\ 0 & 0 &K_{21}^2 & K_{22}^2 & K_{23}^2 & K_{24}^2 \\ 0 & 0 &K_{31}^2 & K_{32}^2 & K_{33}^2 & K_{34}^2 \\ 0 & 0 &K_{41}^2 & K_{42}^2 & K_{43}^2 & K_{44}^2 \\ \end{pmatrix} % \end{array}$$
Se le suma $\mathbf{K}^2_G$ a la matriz $\mathbf{K}$

2.3. Iterar por Elementos (K 3):
$$\mathbf{K^3} = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} K_{11}^3 & K_{12}^3 & K_{13}^3 & K_{14}^3\\ K_{21}^3 & K_{22}^3 & K_{23}^3 & K_{24}^3\\ K_{31}^3 & K_{32}^3 & K_{33}^3 & K_{34}^3\\ K_{41}^3 & K_{42}^3 & K_{43}^3 & K_{44}^3\\ \end{pmatrix} % \end{array} \implies$$$$ \mathbf{K}^3_G = \begin{array}{cc}% & \begin{matrix} u_1\;\; & v_1\;\; & u_2\;\; & v_2\;\; & u_3\;\; & v_3\;\; \end{matrix} \\ \begin{matrix} F_{u_1} \\ F_{v_1} \\ F_{u_2} \\ F_{v_2} \\ F_{u_3} \\ F_{v_3} \end{matrix} & \begin{pmatrix} K_{11}^3 & K_{12}^3 & 0 & 0 & K_{13}^3 & K_{14}^3 \\ K_{21}^3 & K_{22}^3 & 0 & 0 & K_{23}^3 & K_{24}^3 \\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ K_{31}^3 & K_{32}^3 & 0 & 0 & K_{33}^3 & K_{34}^3 \\ K_{41}^3 & K_{42}^3 & 0 & 0 & K_{43}^3 & K_{44}^3 \\ \end{pmatrix} % \end{array}$$
Se le suma $\mathbf{K}^3_G$ a la matriz $\mathbf{K}$

2. Aplicación de Condiciones de Borde (Restricciones) 🚫
#

La matriz $\mathbf{K}$ ensamblada representa la estructura antes de aplicar los soportes (apoyos). Para obtener una solución única y físicamente realista, debemos incorporar las condiciones de borde, que son los GDL con desplazamientos conocidos (generalmente cero en los apoyos).

Modelado de Apoyos:
- Apoyo Fijo (Pinned): $u_x = 0, u_y = 0$.
- Apoyo Móvil (Roller): Restringe el desplazamiento perpendicular a la superficie de rodadura (e.g., $u_y = 0$).
- Empotramiento (Fixed): $u_x = 0, u_y = 0, \theta_z = 0$ (para vigas/marcos).
Partición del Sistema: El sistema global $\mathbf{K} \mathbf{u} = \mathbf{f}$ se puede particionar conceptualmente separando los GDL libres (desplazamientos incógnitos $\mathbf{u}_L$) de los GDL restringidos (desplazamientos conocidos $\mathbf{u}_R$, usualmente $\mathbf{0}$).
$$ \begin{pmatrix} \mathbf{K}\cdot{LL} & \mathbf{K}\cdot{LR} \\ \mathbf{K}\cdot{RL} & \mathbf{K}\cdot{RR} \end{pmatrix} \begin{pmatrix} \mathbf{u}_L \\ \mathbf{u}_R \end{pmatrix} = \begin{pmatrix} \mathbf{f}_L \\ \mathbf{f}_R \end{pmatrix} $$
Donde:
- $\mathbf{u}_L$: Desplazamientos incógnitos (libres).
- $\mathbf{u}_R$: Desplazamientos conocidos (restringidos).
- $\mathbf{f}_L$: Fuerzas aplicadas en los GDL libres.
- $\mathbf{f}_R$: Fuerzas de reacción desconocidas en los GDL restringidos.
Reducción de la Matriz: Para encontrar los desplazamientos incógnitos ($\mathbf{u}_L$), solo necesitamos la primera fila de ecuaciones de la matriz particionada:
$$\mathbf{K}_{LL} \mathbf{u}_L + \mathbf{K}_{LR} \mathbf{u}_R = \mathbf{f}_L$$
Como $\mathbf{u}_R$ es conocido (usualmente $\mathbf{u}_R = \mathbf{0}$), el sistema se reduce a:
$$\mathbf{K}_{LL} \mathbf{u}_L = \mathbf{f}_L - \mathbf{K}_{LR} \mathbf{u}_R$$
Si $\mathbf{u}_R = \mathbf{0}$, simplemente resolvemos:
$$\mathbf{K}_{LL} \mathbf{u}_L = \mathbf{f}_L$$
Llamamos a $\mathbf{K}_{LL}$ la Matriz de Rigidez Reducida ($\mathbf{K}_{\text{red}}$) y $\mathbf{f}_L$ el vector de fuerzas reducido ($\mathbf{f}_{\text{inc}}$). La eliminación de filas y columnas correspondientes a los GDL restringidos es la implementación práctica de esta reducción.

[Diagrama mostrando matriz K particionada y K_LL extraída]

3. Solución Numérica 💡
#

Una vez obtenido el sistema reducido $\mathbf{K}_{\text{red}} \mathbf{u}_{\text{inc}} = \mathbf{f}_{\text{inc}}$, este es un sistema de ecuaciones lineales estándar de la forma $A x = b$.

Herramienta de Solución: La forma más eficiente y numéricamente estable de resolver este sistema es utilizando la función numpy.linalg.solve:

import numpy as np
# K_red: Matriz de rigidez reducida (Numpy array)
# f_inc: Vector de fuerzas reducido (Numpy array)

u_inc = np.linalg.solve(K_red, f_inc)

Evitar la Inversa: Aunque matemáticamente $\mathbf{u}_{\text{inc}} = \mathbf{K}_{\text{red}}^{-1} \mathbf{f}_{\text{inc}}$, calcular explícitamente la inversa ($\mathbf{K}_{\text{red}}^{-1}$) es computacionalmente más costoso y menos estable numéricamente que usar métodos directos como la descomposición LU (implementada en solve). Por lo tanto, np.linalg.solve es la opción preferida.

4. Ejercicio Demostrativo: Armadura Simple de 2 Barras 💻
#

Analicemos una armadura simple de 2 barras conectadas en un nudo y apoyadas en los otros extremos.

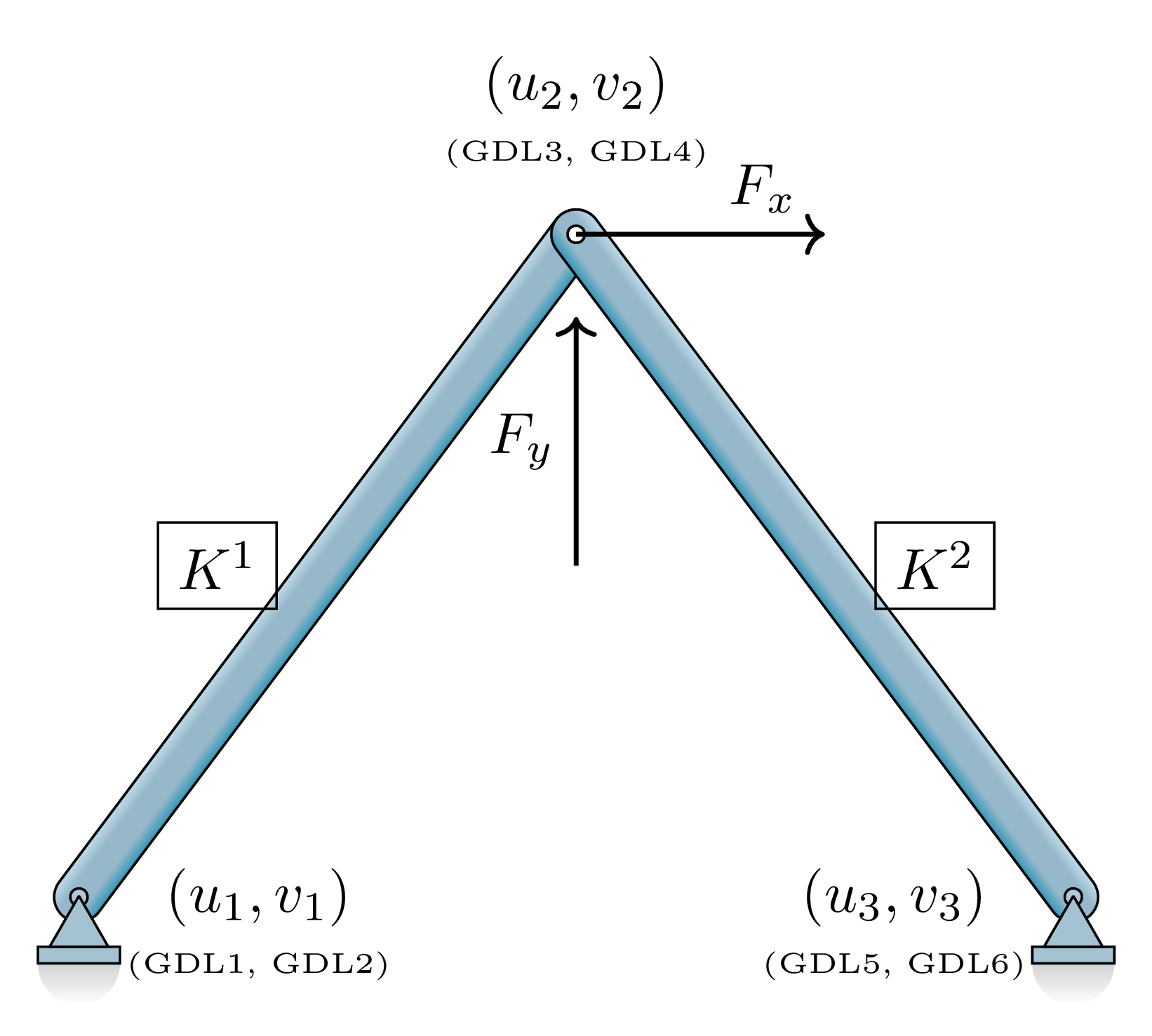
Datos:

Nudo 1: $(0, 0)$, Apoyo Fijo ($U_{1x}=0, U_{1y}=0$). GDL 1, 2.
Nudo 2: $(L, H)$, Libre. Carga $(F_x, F_y)$. GDL 3, 4.
Nudo 3: $(2L, 0)$, Apoyo Fijo ($U_{3x}=0, U_{3y}=0$). GDL 5, 6.
Barra 1 (1-2): Longitud $L_1$, Ángulo $\theta_1$.
Barra 2 (3-2): Longitud $L_2$, Ángulo $\theta_2$.
Propiedades: Mismo $A, E$ para ambas barras.

Pasos:

Calcular $\mathbf{K}_{\text{global}}^{(1)}$ para Barra 1 (GDL involucrados: 1, 2, 3, 4).
Calcular $\mathbf{K}_{\text{global}}^{(2)}$ para Barra 2 (GDL involucrados: 5, 6, 3, 4).
Ensamblar $\mathbf{K}$ global (6x6): Sumar las contribuciones en las posiciones correspondientes. Notar que los GDL 3 y 4 reciben aportes de ambas barras.
Definir $\mathbf{f}$ global (6x1): Solo $f_3=F_x, f_4=F_y$ son no nulos.
Aplicar Condiciones de Borde: GDL restringidos son 1, 2, 5, 6 ($\mathbf{u}_R = \mathbf{0}$). GDL libres son 3, 4 ($\mathbf{u}_L = [U_{2x}, U_{2y}]^T$).
Reducir el sistema: Extraer $\mathbf{K}_{\text{red}}$ ($2 \times 2$, correspondiente a GDL 3 y 4) y $\mathbf{f}_{\text{inc}}$ ($2 \times 1$, correspondiente a GDL 3 y 4). $$\mathbf{K}_{\text{red}} = \begin{pmatrix} K_{33} & K_{34} \\ K_{43} & K_{44} \end{pmatrix}$$ $$\mathbf{f}_{\text{inc}} = \begin{pmatrix} F_x \\ F_y \end{pmatrix}$$
Resolver: Calcular $\mathbf{u}_{\text{inc}} = \mathbf{K}_{\text{red}}^{-1} \mathbf{f}_{\text{inc}}$ usando np.linalg.solve.

import numpy as np

def calcular_K_global(A, E, L, theta_grados):
    # (Función definida en la Sección I para obtener K_global 4x4)
    AE_L = (A * E) / L
    angulo_rad = np.radians(theta_grados)
    c = np.cos(angulo_rad)
    s = np.sin(angulo_rad)
    c2 = c**2
    s2 = s**2
    cs = c * s
    K_g = AE_L * np.array([
        [ c2,  cs, -c2, -cs],
        [ cs,  s2, -cs, -s2],
        [-c2, -cs,  c2,  cs],
        [-cs, -s2,  cs,  s2]
    ])
    return K_g

# --- Datos del Problema ---
L = 4.0 # m
H = 3.0 # m
A = 0.001 # m^2
E = 210e9 # Pa (Acero)
Fx = 5000 # N
Fy = -10000 # N

# Geometría y Propiedades de Elementos
# Barra 1 (Nudo 1 a Nudo 2)
L1 = np.sqrt(L**2 + H**2)
theta1_rad = np.arctan2(H, L)
theta1_deg = np.degrees(theta1_rad)
gdl_1 = [0, 1, 2, 3] # Indices globales para K_global_1 (0-based)

# Barra 2 (Nudo 3 a Nudo 2)
L2 = np.sqrt(L**2 + H**2) 
theta2_rad = np.arctan2(H, -L) # Angulo desde Nudo 3 a Nudo 2
theta2_deg = np.degrees(theta2_rad)
gdl_2 = [4, 5, 2, 3] # Indices globales para K_global_2 (0-based)

# --- Ensamblaje ---
num_gdl_total = 6 
K_global_ensamblada = np.zeros((num_gdl_total, num_gdl_total))

# Calcular K_global para cada barra
K_global_1 = calcular_K_global(A, E, L1, theta1_deg)
K_global_2 = calcular_K_global(A, E, L2, theta2_deg)

# Ensamblar K_global_1
for i_local, i_global in enumerate(gdl_1):
    for j_local, j_global in enumerate(gdl_1):
        K_global_ensamblada[i_global, j_global] += K_global_1[i_local, j_local]

# Ensamblar K_global_2
for i_local, i_global in enumerate(gdl_2):
    for j_local, j_global in enumerate(gdl_2):
        K_global_ensamblada[i_global, j_global] += K_global_2[i_local, j_local]

# --- Definir Vector de Fuerzas Global ---
f_global = np.zeros(num_gdl_total)
f_global[2] = Fx # Fuerza en GDL 3 (U_2x)
f_global[3] = Fy # Fuerza en GDL 4 (U_2y)

# --- Aplicar Condiciones de Borde y Reducir ---
# GDL libres: 2, 3 (U_2x, U_2y)
# GDL restringidos: 0, 1, 4, 5
gdl_libres = [2, 3]
gdl_restringidos = [0, 1, 4, 5]

# Extraer K_red (K_LL)
K_red = K_global_ensamblada[np.ix_(gdl_libres, gdl_libres)]

# Extraer f_inc (f_L)
f_inc = f_global[gdl_libres]

# --- Resolver para Desplazamientos Incógnitos ---
u_inc = np.linalg.solve(K_red, f_inc)

print("--- Resultados del Análisis ---")
print("Matriz de Rigidez Global K (Completa 6x6):")
# print(K_global_ensamblada) # Descomentar para verla completa
print("\nMatriz Reducida K_red (2x2):")
print(K_red)
print("\nVector de Fuerzas Incógnitas f_inc (2x1):")
print(f_inc)
print("\nDesplazamientos Incógnitos u_inc (U_2x, U_2y):")
print(u_inc) # Unidades: metros

7. Ejercicios Propuestos 📝
#

Concepto: Explica por qué la matriz $\mathbf{K}$ global es generalmente rala (sparse, con muchos ceros).
Mapeo: Para una armadura triangular con nudos 1(0,0), 2(L,0), 3(L/2, H), numera los GDL globales (1 a 6) y escribe los vectores de índices globales para cada una de las 3 barras.
Ensamblaje Manual: Dados $\mathbf{K}_{\text{global}}^{(1)}$ ($4 \times 4$ para GDL [0,1,2,3]) y $\mathbf{K}_{\text{global}}^{(2)}$ ($4 \times 4$ para GDL [2,3,4,5]), escribe cómo calcularías el término $K_{33}$ de la matriz global $\mathbf{K}$ (6x6).
Vector F: Para la armadura del ejercicio 2, si se aplica una fuerza vertical $-P$ en el nudo 3 y una fuerza horizontal $Q$ en el nudo 2, escribe el vector $\mathbf{f}$ global (6x1).
Condiciones de Borde: Si el nudo 1 está fijo y el nudo 2 tiene un apoyo de rodillo vertical (restringe $U_{2y}$), ¿cuáles son los GDL libres y restringidos para la armadura del ejercicio 2?
Reducción Manual: Dada una matriz $\mathbf{K}$ (4x4) y $\mathbf{f}$ (4x1), si los GDL 0 y 2 están restringidos a cero, escribe la $\mathbf{K}_{\text{red}}$ (2x2) y $\mathbf{f}_{\text{inc}}$ (2x1) resultantes.
Programación: Adapta el código del ejercicio demostrativo para una armadura donde la Barra 2 (3-2) tiene el doble de área ($2A$).
Programación: Adapta el código del ejercicio demostrativo si el Nudo 3 es un apoyo de rodillo vertical (solo $U_{3y}=0$). ¿Cuáles serían los gdl_libres y gdl_restringidos?
Concepto: ¿Qué significa físicamente que la matriz $\mathbf{K}_{\text{red}}$ sea singular (determinante cero)? ¿Qué implicaría para la estructura?
Interpretación: Si el resultado u_inc del ejercicio demostrativo es [0.001, -0.002], ¿qué significa esto físicamente para el Nudo 2?
Programación: Modifica el código para calcular $\mathbf{K}_{\text{global}}$ de la Barra 1 si su ángulo es $\theta_1 = -30^\circ$.
Ensamblaje: Considera una barra vertical (Nudo 1 a Nudo 2) y una horizontal (Nudo 2 a Nudo 3). Nudo 1 fijo, Nudo 3 fijo. Nudo 2 libre con carga F. Dibuja el sistema, numera GDL y describe qué términos de $\mathbf{K}_{\text{global}}^{(1)}$ y $\mathbf{K}_{\text{global}}^{(2)}$ se sumarían en la $\mathbf{K}$ global.
Concepto: ¿Qué parte del proceso (cálculo de K_global, ensamblaje, reducción, solución) cambiaría si el material de una barra fuera diferente (distinto E)?
Concepto: ¿Qué parte del proceso cambiaría si la carga F se aplicara en medio de una barra en lugar de en un nudo? (Pista: requiere concepto de cargas equivalentes nodales, no cubierto aquí pero importante).
Programación: Escribe una función Python ensamblar(K_global_ensamblada, K_elem, gdl_elem) que tome la K global, la K del elemento y su vector de GDL, y realice la suma/superposición.
Concepto: ¿Por qué es importante usar una numeración de GDL consistente en toda la estructura?
Aplicación: Si el Nudo 2 del ejercicio demostrativo tuviera un asentamiento (desplazamiento impuesto) de $-0.005$ m en la dirección Y, ¿cómo modificarías el vector $\mathbf{f}_{\text{inc}}$ usando la ecuación completa $\mathbf{K}_{LL} \mathbf{u}_L = \mathbf{f}_L - \mathbf{K}_{LR} \mathbf{u}_R$? (Asume $u_{2y}$ ahora es conocido y pertenece a $\mathbf{u}_R$).
Concepto: Explica la diferencia entre resolver $\mathbf{K} \mathbf{u} = \mathbf{f}$ y el análisis de valores propios $\mathbf{K} \mathbf{\phi} = \lambda \mathbf{M} \mathbf{\phi}$ (análisis modal/vibraciones).
Programación: Verifica que la matriz K_global_ensamblada obtenida en el ejercicio demostrativo es simétrica usando np.allclose(K, K.T).
Desafío: ¿Cómo adaptarías el proceso de ensamblaje si los GDL globales no estuvieran numerados secuencialmente (ej. [1, 2, 5, 6] en lugar de [0, 1, 2, 3])?