IV. Generalización 🚀#
Esta sección demuestra la versatilidad del Método de la Rigidez, mostrando cómo el mismo algoritmo de ensamblaje y solución se aplica a estructuras que poseen diferentes Grados de Libertad (GDL) y modos de deformación (axial vs. flexión).
A. Armaduras 2D (Trusses)#
Las armaduras son estructuras que solo transmiten fuerza axial. Utilizan la matriz \(\bar{\mathbf{k}}\) de la barra axial \(4 \times 4\) desarrollada en la Sección I.
GDL Nodal#
- Cada nudo posee dos GDL: Desplazamiento horizontal (\(u_x\)) y Desplazamiento vertical (\(u_y\)).
- Elemento: 4 GDL totales.
Aplicación Práctica: Estructura Triangular (Mapeo \(6 \times 6\))#
El ensamblaje para armaduras sigue la superposición directa de la matriz \(4 \times 4\) del elemento barra dentro de la matriz global \(\mathbf{K}\) del sistema (\(6 \times 6\) para un triángulo), reforzando el concepto de suma en las GDL compartidas.
B. Vigas Sometidas a Flexión (Beam Elements)#
El análisis de vigas introduce la capacidad de un elemento para resistir momentos y deformaciones por flexión.
GDL Nodal#
- Cada nudo posee dos GDL: Desplazamiento vertical (\(v\)) y Rotación (\(\theta\)).
- Elemento: 4 GDL totales (dos por nudo).
Matriz de Rigidez Local del Elemento (\(\mathbf{k}'_{\text{viga}}\))#
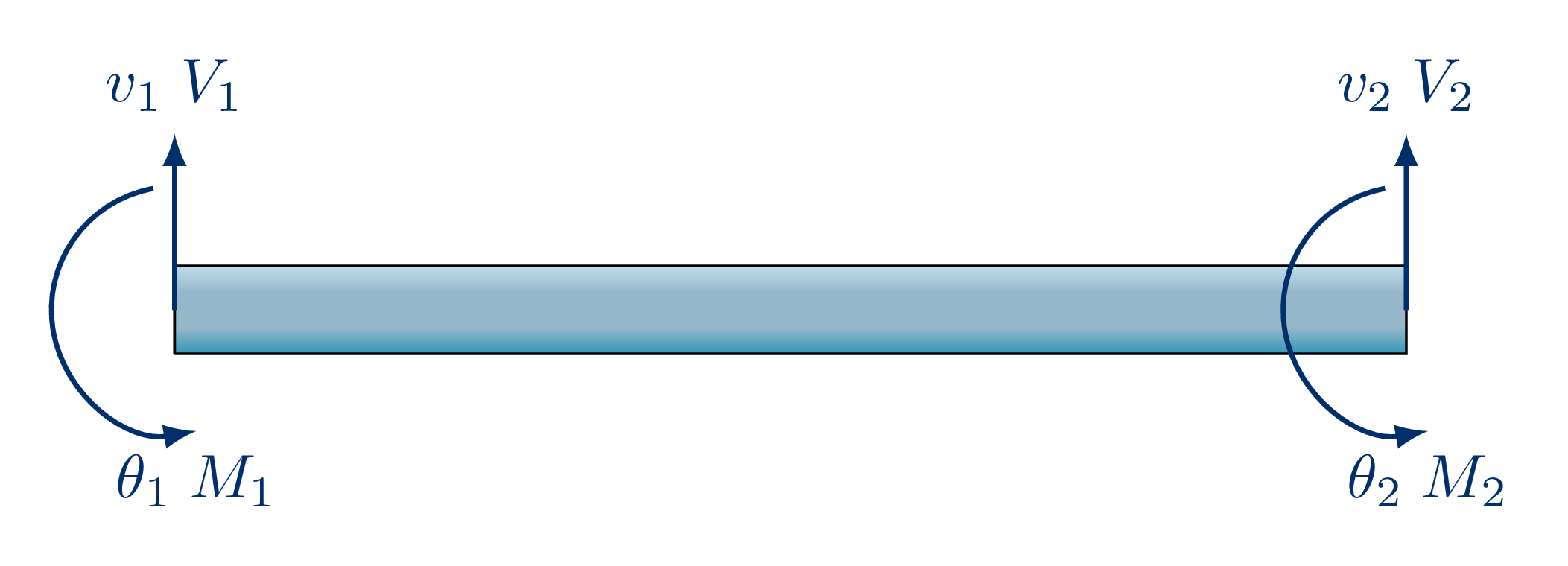
La matriz de rigidez local para flexión relaciona las fuerzas cortantes (\(V\)) y los momentos (\(M\)) nodales con los desplazamientos verticales (\(v\)) y las rotaciones (\(\theta\)). Depende de la rigidez a flexión (\(EI\)).
$$\begin{pmatrix} V_1 \\ M_1 \\ V_2 \\ M_2 \end{pmatrix} = \mathbf{k}'_{\text{viga}} \begin{pmatrix} v_1 \\ \theta_1 \\ v_2 \\ \theta_2 \end{pmatrix}$$$$\mathbf{k}'_{\text{viga}} = \frac{EI}{L^3} \begin{pmatrix} 12 & 6L & -12 & 6L \\ 6L & 4L^2 & -6L & 2L^2 \\ -12 & -6L & 12 & -6L \\ 6L & 2L^2 & -6L & 4L^2 \end{pmatrix}$$
Esta matriz solo considera cargas aplicadas en los nudos. Las cargas en el tramo de la viga (distribuidas o puntuales) se incorporan mediante cargas nodales equivalentes, que se presentan en la Sección V junto con un ejemplo completo de viga continua.
C. Generalización a Marcos y Vigas Inclinadas (6 GDL)#
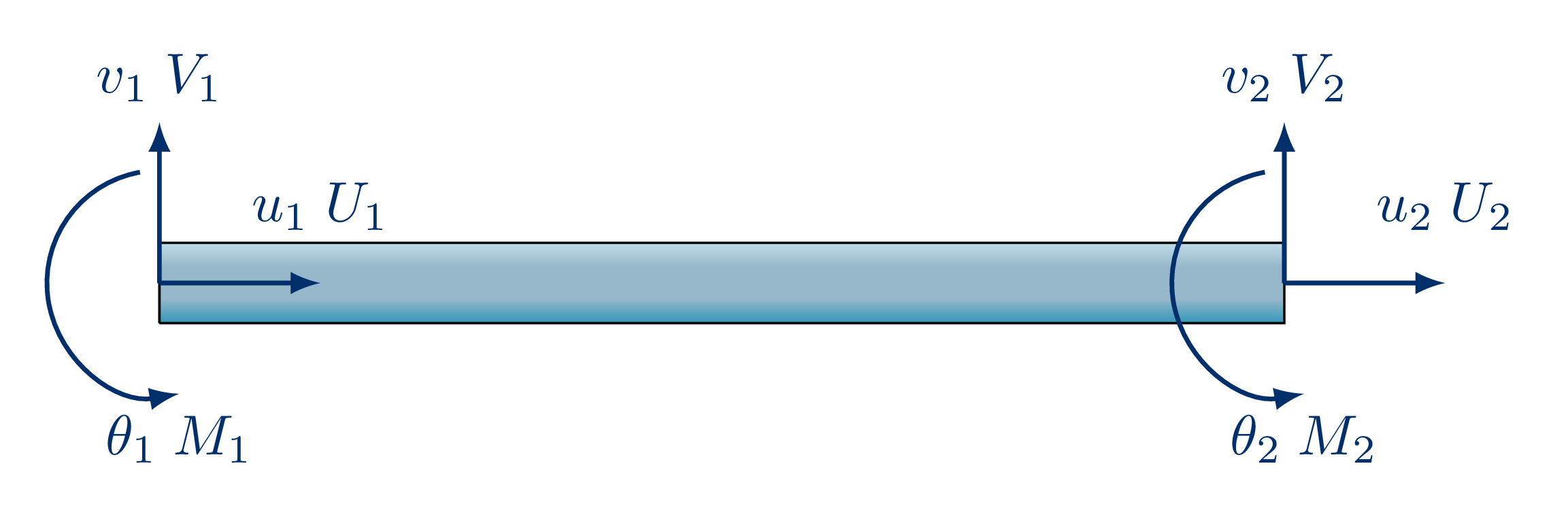
Cuando el elemento no es horizontal (como en un marco o un pórtico), sus ejes locales ya no coinciden con los globales: el desplazamiento transversal local \(v'\) depende de ambos desplazamientos globales \(U_x\) y \(U_y\). Por eso, para un elemento inclinado no bastan los 4 GDL de la viga de la sección B: se utiliza un elemento de marco con 6 GDL (3 por nudo: \(u_x, u_y, \theta\)), que combina los efectos axial y de flexión.
1. La Matriz de Transformación del Marco (\(\mathbf{T}_{\text{marco}}\))#
Sean \(c = \cos\alpha\) y \(s = \sin\alpha\), con \(\alpha\) el ángulo del elemento respecto al eje \(X\) global (se usa \(\alpha\) para no confundirlo con la rotación nodal \(\theta\)). En cada nudo, los desplazamientos locales se obtienen proyectando los desplazamientos globales sobre los ejes locales \(x'\) (axial) e \(y'\) (transversal):
$$u' = c\,U_x + s\,U_y \qquad v' = -s\,U_x + c\,U_y \qquad \theta' = \Theta$$La rotación no cambia con el sistema de coordenadas: en el plano, ambos sistemas giran en torno al mismo eje \(z\), por lo que \(\theta\) es un escalar.
Ordenando los GDL como \([u_1, v_1, \theta_1, u_2, v_2, \theta_2]\), la transformación del elemento completo es:
$$\begin{pmatrix} u'_1 \\ v'_1 \\ \theta'_1 \\ u'_2 \\ v'_2 \\ \theta'_2 \end{pmatrix}_{\text{local}} = \mathbf{T}_{\text{marco}} \begin{pmatrix} U_{1x} \\ U_{1y} \\ \Theta_1 \\ U_{2x} \\ U_{2y} \\ \Theta_2 \end{pmatrix}_{\text{global}} \qquad \mathbf{T}_{\text{marco}} = \begin{pmatrix} c & s & 0 & 0 & 0 & 0 \\ -s & c & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & c & s & 0 \\ 0 & 0 & 0 & -s & c & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}$$\(\mathbf{T}_{\text{marco}}\) es ortogonal (\(\mathbf{T}^{-1} = \mathbf{T}^T\)): solo rota los ejes, no cambia longitudes.
Nota: Para una viga horizontal (\(\alpha = 0^\circ\)) se tiene \(c = 1\), \(s = 0\) y \(\mathbf{T}_{\text{marco}} = \mathbf{I}\): los ejes locales y globales coinciden. Si además la viga no tiene carga axial, se pueden usar solo los 4 GDL \((v, \theta)\) de la sección B. Para un elemento inclinado esto ya no es posible, porque \(v'\) depende también de \(U_x\): no existe una transformación que use únicamente \(U_y\) y \(\Theta\).
2. Matriz de Rigidez del Elemento en Ejes Globales (Generalizada)#
La matriz de rigidez en ejes globales para un elemento inclinado que considera ambos efectos (axial y flexión) se obtiene de la misma manera:
$$\bar{\mathbf{k}}_{\text{marco}} = \mathbf{T}_{\text{marco}}^T \mathbf{k}'_{\text{marco}} \mathbf{T}_{\text{marco}}$$Donde \(\mathbf{k}'_{\text{marco}}\) es una matriz local \(6 \times 6\) que combina la rigidez axial y la rigidez de la viga en un solo elemento.
D. Ejercicio Demostrativo en Python: Matriz de Rigidez de un Elemento de Marco (Viga + Axial) 💻#
Para demostrar la generalización, mostraremos la matriz local \(6 \times 6\) que combina las rigideces axial y a flexión.
GDL Ordenados (Local): \([u'_1, v'_1, \theta'_1, u'_2, v'_2, \theta'_2]\)
import numpy as np
# Datos de la Viga
E = 200e9 # Pa
I = 0.0005 # m^4
A = 0.01 # m^2 (Necesario para el efecto Axial)
L = 5.0 # m
# Coeficientes de Rigidez
AE_L = (A * E) / L # Rigidez Axial
EI_L3 = (E * I) / (L**3) # Rigidez de Flexión (Cortante)
EI_L2 = (E * I) / (L**2) # Rigidez de Flexión (Momento-Cortante)
EI_L = (E * I) / L # Rigidez Rotacional
# Matriz de Rigidez Local del Marco (6x6)
# El orden [u'1, v'1, theta'1, u'2, v'2, theta'2] permite combinar Axial (u') y Flexión (v', theta').
k_axial = np.array([
[AE_L, 0, 0, -AE_L, 0, 0], # Interacciones u'1
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[-AE_L, 0, 0, AE_L, 0, 0], # Interacciones u'2
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0]
])
k_viga = np.array([
[0, 0, 0, 0, 0, 0],
[0, 12 * EI_L3, 6 * EI_L2, 0, -12 * EI_L3, 6 * EI_L2], # Interacciones v'1
[0, 6 * EI_L2, 4 * EI_L, 0, -6 * EI_L2, 2 * EI_L], # Interacciones theta'1
[0, 0, 0, 0, 0, 0],
[0, -12 * EI_L3, -6 * EI_L2, 0, 12 * EI_L3, -6 * EI_L2],# Interacciones v'2
[0, 6 * EI_L2, 2 * EI_L, 0, -6 * EI_L2, 4 * EI_L] # Interacciones theta'2
])
# Suma: k_local_marco = k_axial + k_viga
k_local_marco = k_axial + k_viga
print("--- Matriz de Rigidez Local del Elemento de Marco (6x6) ---")
np.set_printoptions(precision=2, suppress=True, linewidth=150)
print(k_local_marco)
# Verificación de un elemento inclinado (ej. 45 grados)
angulo_grados = 45.0
angulo_rad = np.radians(angulo_grados)
c = np.cos(angulo_rad)
s = np.sin(angulo_rad)
T_marco = np.array([
[c, s, 0, 0, 0, 0],
[-s, c, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, c, s, 0],
[0, 0, 0, -s, c, 0],
[0, 0, 0, 0, 0, 1]
])
k_elem_inclinado = T_marco.T @ k_local_marco @ T_marco
print("\n--- Matriz del elemento a 45° en ejes globales (T^T * k_local * T) ---")
print(k_elem_inclinado)
Con tu Módulo rigidez.py 🧰#
La función k_marco reúne el ejercicio demostrativo en una sola función: arma \(\mathbf{k}'_{\text{marco}}\), construye \(\mathbf{T}_{\text{marco}}\) a partir de las coordenadas de los nudos y entrega \(\bar{\mathbf{k}}_{\text{marco}}\). Agrégala a tu rigidez.py:
# ============================ Sección IV ============================
def k_marco(A, E, I, xy1, xy2):
"""Matriz de rigidez 6x6 de un elemento de marco en ejes globales.
GDL por nudo: (ux, uy, θ). Combina la rigidez axial y la de flexión.
"""
L, c, s = geometria_barra(xy1, xy2)
a = A * E / L
b = E * I / L**3
k_local = np.array([
[ a, 0, 0, -a, 0, 0],
[ 0, 12*b, 6*L*b, 0, -12*b, 6*L*b],
[ 0, 6*L*b, 4*L**2*b, 0, -6*L*b, 2*L**2*b],
[-a, 0, 0, a, 0, 0],
[ 0, -12*b, -6*L*b, 0, 12*b, -6*L*b],
[ 0, 6*L*b, 2*L**2*b, 0, -6*L*b, 4*L**2*b],
])
T = np.zeros((6, 6))
T[:3, :3] = T[3:, 3:] = [[ c, s, 0],
[-s, c, 0],
[ 0, 0, 1]]
return T.T @ k_local @ T
Verifiquemos que entrega la misma matriz que el ejercicio demostrativo:
import numpy as np
from rigidez import k_marco
# Elemento de 5 m a 45°: debe coincidir con k_elem_inclinado
alpha = np.radians(45)
k = k_marco(0.01, 200e9, 0.0005, (0, 0), (5*np.cos(alpha), 5*np.sin(alpha)))
np.set_printoptions(precision=2, suppress=True, linewidth=150)
print(k)
E. Ejercicios Propuestos 📝#
- Marco (GDL): ¿Por qué un elemento de marco necesita 6 GDL, y no 4 como la viga o la barra axial?
- Transformación: Explica por qué, en \(\mathbf{T}_{\text{marco}}\), las filas de las rotaciones tienen un 1 en la diagonal y ceros en el resto. Verifica numéricamente que \(\mathbf{T}_{\text{marco}}^T \mathbf{T}_{\text{marco}} = \mathbf{I}\) para \(\alpha = 30^\circ\).
- Marco (k local): En la matriz \(\mathbf{k}'_{\text{marco}}\), ¿qué términos de la rigidez axial (\(AE/L\)) aparecen en la fila 2 (GDL \(v'_1\))? Justifica tu respuesta.
- Acoplamiento: En la matriz \(\bar{\mathbf{k}}_{\text{marco}}\) de un elemento inclinado, ¿por qué se acoplan \(U_x\) y \(U_y\) (es decir, \(\bar{k}_{12}\) y \(\bar{k}_{21}\) son distintos de cero)? ¿Ocurre lo mismo en un elemento horizontal?
- Programación: Modifica el código demostrativo para un elemento horizontal (\(\alpha = 0^\circ\)). ¿Cómo se compara \(\bar{\mathbf{k}}_{\text{marco}}\) con \(\mathbf{k}'_{\text{marco}}\)?
- Programación: Escribe \(\mathbf{T}_{\text{marco}}\) para un elemento vertical (\(\alpha = 90^\circ\)) y calcula su \(\bar{\mathbf{k}}_{\text{marco}}\). ¿En qué posiciones quedan ahora los términos axiales y los de flexión?
- Concepto: Si se considera el elemento axialmente indeformable (\(A \to \infty\), es decir, \(AE/L \to \infty\)), ¿qué ocurre con los términos axiales de \(\mathbf{k}'_{\text{marco}}\)? ¿Qué problema numérico podría aparecer al resolver el sistema? (Pista: número de condición).
- Ensamblaje y apoyos: Para un marco simple (dos columnas verticales y una viga horizontal), numera los GDL (3 por nudo) e indica qué elementos aportan rigidez en cada nudo superior. ¿Qué GDL se restringen si la base de las columnas está empotrada? ¿Y si es un apoyo fijo (rotulado)?
- Concepto: Explica la diferencia entre un nudo rígido y un nudo articulado en un marco. ¿Qué GDL deja de ser compartido entre los elementos en un nudo articulado?
- Post-procesamiento: En un marco, una vez obtenido el vector de desplazamientos \(\mathbf{u}\) de la estructura, ¿cómo calcularías el cortante \(V\) y el momento \(M\) en el Nudo 1 de un elemento inclinado? (Pista: \(\mathbf{u}'_e = \mathbf{T}_{\text{marco}} \mathbf{U}_e\) y luego \(\mathbf{f}'_e = \mathbf{k}'_{\text{marco}} \mathbf{u}'_e\); si hay cargas en el tramo, resta \(\mathbf{f}'_{\text{eq}}\) como en la Sección V).